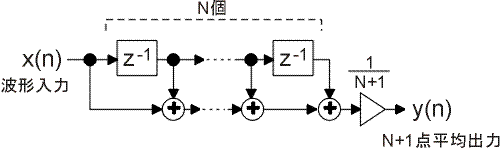
算術平均の直接実現
過去の信号入力を何点か平均して出力するフィルタを考えます。 図のようにN個の遅延を用いることで、現在の入力値からN個前の入力値までの和を 計算し、(N+1)で割ることで、(N+1)点平均を行うことができます。

この(N+1)点分の和を求める操作は、図に示す手法を用いると、 より効率的に行うことができます。
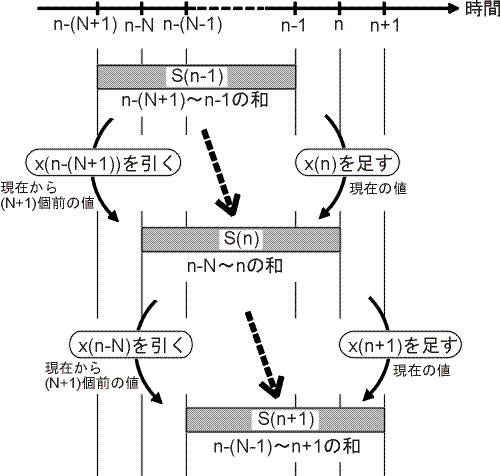
すなわち、ある時刻において過去(N+1)点分の和を求めて保存しておけば、 その後の時刻における過去(N+1)点分の和は、保存してある和の値に対して、 順次「現在から(N+1)個前の値を引き算して、現在の値を足し算する」処理を 繰り返せば求められることになります。この場合、1ステップ当り必要な 演算回数は、N点平均を直接行う場合にN回の足し算が必要になるのに比べて、 1回の足し算と1回の引き算だけで済んでしまうため、プログラムの効率が 非常に良くなります。
(作成: 2000年7月19日, 最終更新: 2000年10月31日)